敌手模型
[!info] 参考敌手模型
最近看到有将差分隐私和同态加密结合到联邦学习中,所以想问下为啥现有的一些研究需要同时用到这两种保护法?– 知乎
是否需要叠加运用差分隐私,完全取决于敌手模型的余下部分:存在某些想要窥探其他客户端隐私的客户端吗?模型最后还会发布给第三方吗?
如果回答都是否定的,差分隐私,甚至是任何防御技术都是多余的,因为已经没有额外的敌手需要防御了(但这种情况太理想了)。
如果前一个问题成立,那么存在一个“A 客户端的信息可能从每轮的全局更新中泄露给另一个客户端 B”的问题。如果后一个问题成立,那么存在一个“A 客户端的信息可能从最终模型中泄露给第三方 C”的问题。无论是哪种情况(抑或是两种情况的叠加),我们就需要考虑“如何避免这些渠道带来的信息泄露机会”。注意到这些渠道都是必须的、不能直接关闭的:我们不得不让客户端 B 看到全局更新,否则它没法参与训练;也不得不让第三方看到最终的模型,否则不必假设它的存在。此时,我们能做到的最好的,就是牺牲这些渠道的信噪比,通过让敌手知道点什么又不知道点什么,换来必要的隐私保护——这就是差分隐私能够实现的。为了使用差分隐私,可以让每个客户端在每轮上传其本地更新前往其中加一小份噪声,从而使得全局聚合更新中的噪声达到设定的水平,这是所谓的分布式差分隐私(distributed DP)。考虑到不是每个客户端都诚实地做到这件事情(”存在服务器 - 客户端共谋“的假设蕴涵了这个事实),一个更安全的做法是让每个客户端在自己上传的本地更新就加了足够保护隐私的噪声,这是所谓的局部隐私(local DP)。
防御目标
[!INFO]+ 数据隐私
当一个查询者需要查询数据库中数据时(这一操作我们用 表示),由于安全机制存在,他无法获取到整个数据库完整的数据,而只能得到一些加工过的数据(例如计数,均值,众数)。但即便是这样的查询方式依旧会导致隐私的泄漏,例如查询者查询到某医院早上患 A 病人数为 ,而通过其他方式得知该医院今天只出院一人为张三,同时下午查询患 A 病人数变为 ,则可推断出张三患 A 病。而加入差分隐私后,每次查询都将引入一个噪声 B,例如这样使得查询者早上、下午均只能查询到患 A 病人数为 人,则张三的隐私得以被保护。 【1】差分隐私创始人哈佛大学教授 Cynthia Dwork 的定义
[!INFO]+ 达勒纽斯愿望(Dalenius Desideratum)
由统计学家 Tore Dalenius 提出的隐私保护理想,强调数据发布不应增加对个人隐私的任何风险,即数据发布后,攻击者对个人的了解不应超过数据发布前。任何有用的模型都无法完全满足这一要求。这是因为:
- 模型的实用性:为了使模型有用,它必须从输入数据中学习和提取信息,以提供有意义的输出。这意味着模型不可避免地会对输入数据进行某种程度的“曝光”。
- 信息泄露的不可避免性:当模型提供预测、分类或生成数据时,即使只是输出结果,也可能会泄露关于训练数据或输入数据的某些信息。
因此,完全避免模型对输入数据的任何额外信息泄露,在实用的模型中是无法实现的。在认识到达勒纽斯愿望难以实现的情况下,差分隐私 被提出作为一种实用的隐私保护定义。它提供了严格的数学保证,限制了单个数据点对输出的影响。
汉明距离
汉明距离 : 信息论 概念,两个码字之间对应位的不同。在差分隐私中,该该概念表示两个数据集(数据库)在多少个对应位置上存在差异。
[!TIP]+ 汉明距离 (
)与差分隐私
数据集和 ,我们可以计算它们之间的汉明距离和曼哈顿距离。每个数据元组包含三个特征:年龄、收入和邮编。
汉明距离为 2,因为有两个元组(第一个和第二个)在至少一个属性上存在差异。在探讨差分隐私时,除了使用汉明距离衡量数据集
和 之间的差异,我们还可以采用差分隐私的具体定义来描述数据集的相邻关系。对称性差分隐私规定 ,如果两个数据集通过添加或删除单个数据项就能互相转换,则认为它们是 相邻 的;而 非对称性差分隐私 则定义,如果可以通过替换数据集中的一个元素使得两个数据集相等,并且元素数量保持不变,那么这两个数据集也被视为 相邻。这些定义均旨在保护个体数据项的隐私,确保不因数据项的存在、缺失或值的改变而泄露个体信息,从而实现差分隐私的核心目标,而与具体的距离度量无关。
<u> 根据对称性 / 非对称性角度的定义,上述两个数据不是相邻的数据集。</u> ^gbxop1
差分隐私
差分隐私:一种数学技术,向数据集中添加受控数量的随机性,以防止任何人获取有关数据集中的个人信息。
- 变量
: 表示 概率 : 随机算法 , 是用于 处理数据并生成受保护输出 的机制。可以是任何种类的数据处理函数,如求平均值、计数、统计总和等,而且会在这些计算中 嵌入随机性(例如加入满足特定分布的噪声),这种随机性是保障输出不会直接反映输入数据的微小变动的关键. : 输出空间的子集,定义随机算法 输出结果中感兴趣的区域,例如某种统计量的阈值区间. : 由全体数据集 中的元素生成的数据库(为 数据集 ),这两个数据集 汉明距离 小于等于 1, 即 和 至多在一个数据点上有差异。 - 例如: 全集
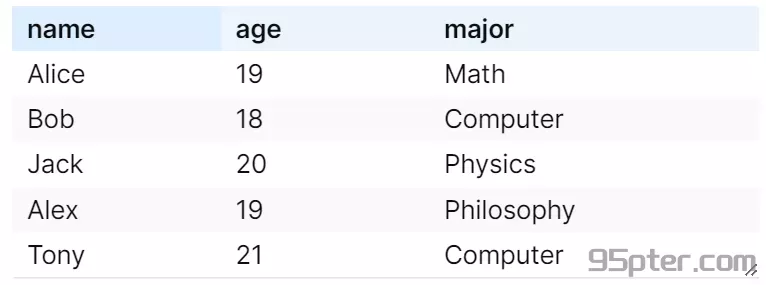
- 令
,数据库 为 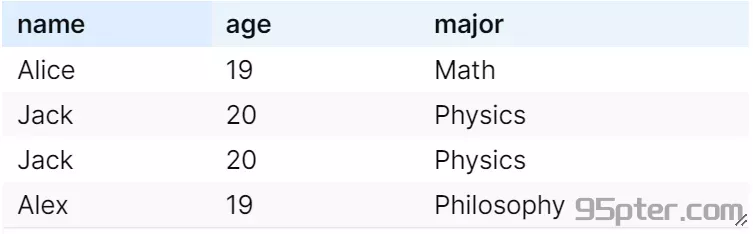
- 例如: 全集
: 隐私预算 - 若
越小,隐私保护能力越强,即算法输出与数据集的微小变化之间的关联性更弱。这意味着数据结果中推断任何单体信息的可能性非常低,但 <u> 可能 </u> 会造成数据集可用性下降。 - 每次进行数据查询时将会降低隐私预算,当
降低为阈值之下时将不再允许查询直至预算被重置或数据集更新。 - ==注意==:
并不直接等于引入的噪声量。 是衡量隐私保护强度的参数,而噪声量取决于 、函数的敏感度以及所采用的隐私放大技术。 - 使用具有 隐私放大效应 的技术(如子采样、个体敏感性),我们可以在 保持
不变 的情况下,减少引入的噪声量,从而提高模型的效用。
- 若
[!QUESTION]- 为什么要求
?
要求两个数据集汉明距离为 1,即它们在严格一个记录上有差异(这种差异可能是增删或者修改)。基于这样的数据集对比,要求算法确保单个数据无论是增加、删除还是修改不会在输出中被检测出来(KL 散度 小于)。
- 噪声 :在保护更大的数据集差异(例如汉明距离大于 1)时,所需要的噪声量会显著增加,这可能会 降低查询结果的准确性和实用性 。而现实生活中, 数据变动通常是局部的(只改变少数几条记录),汉明距离为 1 的标准通常是足够的。为了最小化对于数据实用性影响,选择汉明距离为 1 的数据集作为保护的基准。
- 实际上 我们也不可能保护整个群体的隐私 :(Shokri 等, 2017, p. 3) (pdf) 无法防止的泄露——如果模型基于总体的统计事实,那么防止这种泄露可能是不可能的。
推导
我们并不需要知道完整的分布的差异,而是需要知道输入值
[! info]- 针对最大散度的理解
最大散度关注的是在个给定条件的条件下,针对 的所有取值 集合 中,找到一个 值,使得上式右侧取到最大值,在这个给定取值时, 和 的分布差异最大。
松弛
由于实际应用中需要很多的隐私预算,为了算法实用性,引入松弛版本的差分隐私
:通常为一个非常小的整数 (如 或更小),它定义了算法允许违反 界限的 概率上限。一个非零的 可以在保持合理隐私保护的同时,减少噪声的量,提高查询结果的实用性。 - 满足该式的差分隐私,被称为

[!ABSTRACT]+ 当我们在讨论差分隐私时,我们究竟在讨论什么
当我们说
我们在讨论的是任何两个汉明距离为 1 的数据集
和 ,算法 产生的结果落在集合 中的概率不会因为 和 这一小差异而有大的不同。
Rényi 差分隐私
Rényi 散度
Rényi (瑞丽散度)作为统一所有散度的一个公式,2017 年 Mironov 提出【1】.
: 取 在 分布下的 期望,即平均情况 - 当
时,根据洛必达法则,可得 为 KL 散度,其对应的机制为松弛差分隐私 #TODO(需要厘清的点是这是为什么,松弛项 对应的是 KL 散度中的哪个值) - 当
时,Rényi 散度会收敛到最大散度:
- 对于中间情况,如果 Rényi 散度的值小于
,则称对应的机制满足 -RDP
title: Rényi 散度其他表现公式
1.
$$
\mathbb E \left[L^{(\alpha-1)}
_{\mathcal M,x,x'}
\right]
\leqslant \exp((\alpha-1)\tau)
$$
该公式表示 $\mathcal M$ 机制满足 $(\alpha,\tau)$-RDP
Rényi 差分隐私与差分隐私
对于一个机制
两个输入
则有该机制
[1]Canonne, Kamath 和 Steinke,《The Discrete Gaussian for Differential Privacy》.


