论文主要内容:提出了一个新的散度计算公式,α- 散度(α-divergence)来分析 差分隐私中的子采样隐私增强现象。这种方法能够恢复并改进现有的隐私增强分析结果,同时提供新的隐私增强实例。
论文贡献:
- 证明了子采样后引入加噪机制可以严格提高隐私保护效果(降低
) - 量化 子采样差分隐私机制 (使用 Mechanism
)对隐私保护的放大(Privacy Amplification)的作用, 并证明边界的最优性 - 注:该论文是完全基于数学证明的论文,只作为介绍和扩展使用
前置知识
总变差距离
总变差距离(Total Variation Distance,记作
或者
理解这两个公式:
- 前一个公式可以认为是对两个分布的所有情况,即所有取值
上的差异进行求和后,进行归一化得到 由于两个分布概率总和为 ,所以进行归一化(即除以 2) - 后一个公式可以认为是计算两个分布在所有情况下最小概率之和,然后用总概率减去这个概率,就是有差异的最大概率
高级联合凸性定理
提供了一种 计算两个混合分布之间 差异的方法,通过分析其组成部分的差异,简化了计算。对于两个混合分布:
- 相同的基础分布:
- 不同的成分:
则有
公式
其中
,且
用处
子抽样会导致机制的输出是一个混合分布,直接分析这种混合分布的差异非常困难。高级联合凸性定理提供了一种方法,将对混合分布的分析转化为对其组成部分的分析。这使得计算更简单、更可控。
graph LR
A[分析混合分布]
B[分析混合分布的组成成分]
A--> B
定义
其中
- 用于衡量两个 概率测度
和 之间的差异,也就是两个概率分布的差异 表示对所有可测子集 取上确界(supremum), 表示取正部,即 。
连续与离散情形下
- 连续情形:
差分隐私与
差分隐私的定义可以通过这个散度度量来表达的
若对于所有满足
隐私曲线
隐私曲线 Privacy Profile
若已知一个机制
- 隐私曲线提供了机制
满足 - 差分隐私的所有参数对 。 - 机制
是 - 差分隐私的,当且仅当: 或者说,对于给定的 ,只要 不小于 ,机制 就满足 - 差分隐私。
定义
隐私曲线
$$
\delta_M(\varepsilon) = \sup_{x \sim_X x’} D_{e^\varepsilon}(M(x) | M(x’))
$$
其中
理解
- 直观理解: 隐私曲线描述了机制
在不同的 下需要满足 - 差分隐私所对应的最小 值。 - 隐私参数空间划分: 隐私曲线
将 参数空间划分为两部分: - 当
时,机制 满足 - 差分隐私。 - 当
时,机制 不满足 - 差分隐私。
- 当
- 曲线存在性: 对于任何机制
,隐私曲线 都存在,即使对于某些 值机制满足纯差分隐私(即 )。
群体隐私曲线
- 定义: 对于
,群体隐私曲线 表示在改变 个数据的情况下,机制 的隐私损失。 - 公式: 使用邻接关系
诱导的路径距离 : 其中 是从 到 的最短相邻路径的长度。
总结:
- 隐私曲线 为差分隐私机制提供了一个全面的隐私参数描述,明确了在每个
下机制需要满足的最小 值。 - 与原始
- 差分隐私的关系 在于,隐私曲线为机制是否满足差分隐私提供了直接的判定标准。 - 公式关系 可以概括为:
通过理解隐私曲线,我们可以更好地分析和比较不同机制的隐私特性,设计满足特定隐私要求的算法。
子采样
子采样 Subsampling
使用子采样的原因
将加噪机制应用到子采样中可以提高机制的隐私性
*“A well-known method for increasing privacy of a mechanism is to apply the mechanism to a random subsample of the input database, rather than on the database itself. Intuitively, the method decreases the chances of leaking information about a particular individual because nothing about that individual can be leaked in the cases where the individual is not included in the subsample.”(Balle 等, 2018, p. 3) (pdf) 🔤一种众所周知的提高机制隐私性的方法是将机制应用于输入数据库的随机子样本,而不是数据库本身。直观地说,这种方法可以降低特定个人的信息泄露几率,因为在子样本中不包含该个人的情况下,该个人的任何信息都不会泄露。🔤
定义
子采样 机制
它接受一个数据库
量化
条件
- 给定一个差 分隐私机制
,它对输入 输出一个关于结果空间 的概率分布。 的隐私曲线 描述了机制在不同隐私参数 下的隐私损失。 - 考虑 组合后的机制
,定义为 。 - 对输入数据库
先进行子抽样 ,然后对得到的子样本 应用机制 加入噪声 。
- 对输入数据库
目标
[!info] 找到下面两者之间的关系。
的隐私曲线 的隐私曲线
即希望对于每个
其中
结论
对于所有子采样后引入机制的结果,可以使用下面的式子同一表示其隐私增强的结果
,这个值必然小于等于 - 表明经过子抽样后,机制的隐私参数得到了增强,对应的
也有所改善
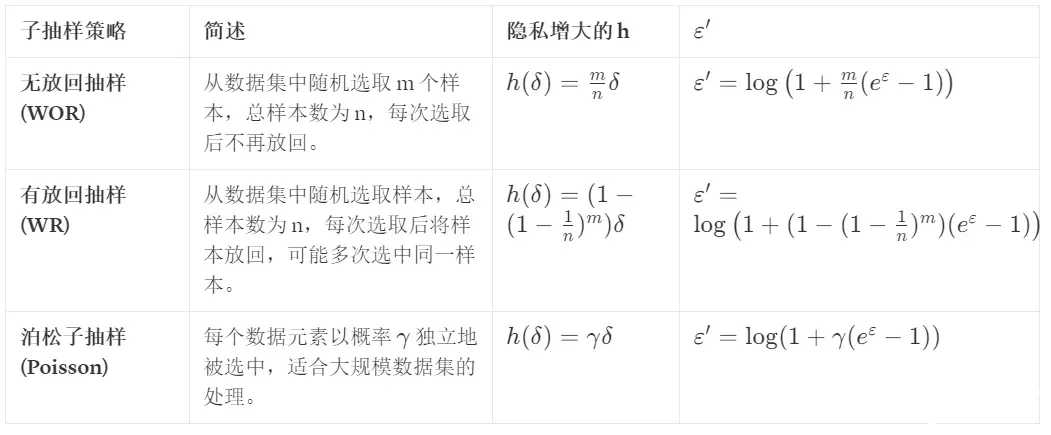
函数
函数
- 子采样的策略:不同的子采样方法,会导致不同的函数形式,整理如下